在开发 Realm 的时候,我们不断地寻找优化速度的方法。这是一个关于我们如何开发一个比 C++ STL 快 24% 的二叉搜索函数的故事。
为什么选择二叉树做搜索?
Realm 以二叉树结构存储数据。比如,假设 Realm 通过以下链表中的 IDs 存储对象:

如果你想要找到 ID 等于 14 的对象,你需要 5 次操作才能找到他,也就是 O(n) 的复杂度。
使用二叉树搜索是提升检索速度的一种方法:
“搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。” -Wikipedia
对象可以存储在二叉树中。二叉树可以通过从根节点遍历树来快速定位对象。基于 IDs 创建的二叉树就像如下这样:
搜索 ID 等于 14 的对象,仅仅只需 3 次操作 ,或者说是 O(log2(N)) 的复杂度。
有这样优秀的性能,二叉树自然而然的成为了 Realm 要去尝试和优化的索引方案。
在 C++ 标准库 (STL) 中有一些二叉树搜索函数,包括 std::lower_bound() 和 std::upper_bound()。我们决定模仿 std::upper_bound() 的操作,同时用他来作为我们测试中的的参考。下方的函数是通过二叉树搜索并且尝试找到第一个比指定元素大,并返回该元素位置的一种写法:
// For a sorted list, vec, return the index of the first element that compares
// greater to the value, or return vec.size() if no such element is found.
size_t match = std::upper_bound(vec.begin(), vec.end(), value) - vec.begin();
比如,用跟上面一样的 IDs 数据,我们传入 value 为 13,调用std::upper_bound() 函数,它将会返回 4,因为 14 是比 13 大的第一个元素。

测试初始化
我们当前目标是移动设备,为了考虑到未来的一些架构,我们选择了以下的设备来做基准测试:


上: 32 位的华为 P7 手机,型号: Huawei Kiri 910T (ARMv7 / Cortex-A9)
下:HP Envy dv6 笔记本,采用 Intel core 64 位 i7-3630QM CPU
我们使用 clang+++ 编译器来编译 iOS, g++ 来编译 Android 和 Linux,Visual Studio 来编译 Windows 版本,因此我们选择了以下的设置:

我们在 ARM 上没有启用 16 位模式,因为 16 位模式对我们的代码而言会损失掉 32 位模式一半的性能。
基准
我们首先研究下 std::upper_bound() 函数来得到一个对比的基准。我们一切类型都用 size_t 类型(简记为 T) 因为他会适配所有的处理器寄存器大小(32 或者 64位)。
我们选择的链表大小为 8192 个元素,占据最多 32 千字节,同时跟 L1 缓存大小相仿。在 x64 架构上,占用两倍于缓存, 64 千字节,因此我们会得到很多的 L1 缓存无法命中。
我们对 std::upper_bound() 函数进行简单的包装,让新函数直接返回 size_t 而不是迭代器。
template <class T> INLINE size_t fast_upper_bound0(const vector<T>& vec, T value)
{
return std::upper_bound(vec.begin(), vec.end(), value) - vec.begin();
}
我们来大概看一眼在 libstdc++ 的 stl_algo.h 头文件中, upper_bound() 实现中的内部循环:
while (__len > 0)
{
_DistanceType __half = __len >> 1;
_ForwardIterator __middle = __first;
std::advance(__middle, __half);
if (__val < *__middle)
__len = __half;
else
{
__first = __middle;
++__first;
__len = __len - __half - 1;
}
}
return __first;
… and benchmark it: … 测试结果如下:

Version 1
我们在看 STL 版本的代码的时候,会发现 if 语句中有两个条件代码块。 第一个只包含一个赋值语句:
__len = __half;
第二个部分包含三条语句:
__first = __middle;
++__first;
__len = __len - __half - 1;
我们先尝试优化一下这个,用两句和一句替代原来的语句:
template <class T> INLINE size_t fast_upper_bound1(const vector<T>& vec, T value)
{
size_t size = vec.size();
size_t i = 0;
size_t size_2 = size;
while (size_2 > 0) {
size_t half = size_2 / 2;
size_t mid = i + half;
T probe = vec[mid];
if (value >= probe) {
i = mid + 1;
size_2 -= half + 1;
}
else {
size_2 = half;
}
}
return i;
}
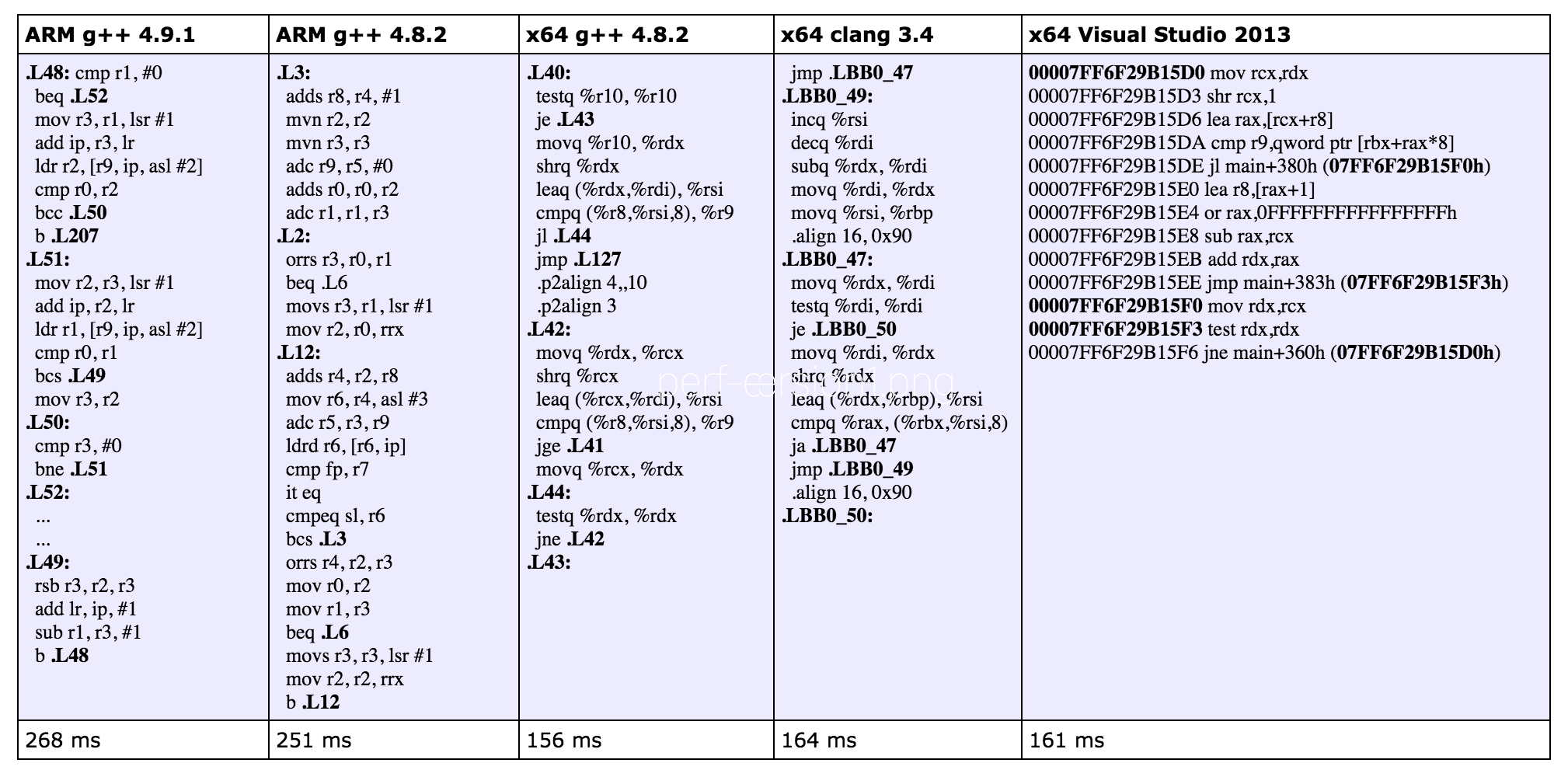
从下面的汇编代码来看,编译器在不同平台生成了不同的代码,每一个分支包含了一个代码块儿,同时还有用分支指令来控制执行的顺序。
这意味着编译器没有对执行流程进行优化调整,如此而言,STL 里的代码在不同平台上性能并没有很大差异。我们可以观察到在 ARM 平台上 g++ 4.9.1 做了一些循环展开,以及将第二个 if 语句放在一个比较远的独立区块里。
Version 2
我们即便尝试简化算法,但是依然包含有两种情况的 if 语句,我们这次尝试着只在 if 语句中做一次简单的赋值操作,并且所有赋值语句有相同的源变量。
template <class T> INLINE size_t fast_upper_bound2(const vector<T>& vec, T value)
{
size_t m_len = vec.size();
size_t low = -1;
size_t high = m_len;
assert(m_len < std::numeric_limits<size_t>::max() / 2);
while (high - low > 1) {
size_t probe = (low + high) / 2;
T v = vec[probe];
if (v > value)
high = probe;
else
low = probe;
}
if (high == m_len)
return m_len;
else
return high;
}
这次改进在 g++ 和 clang 上有了比较明显的速度提升,将分支操作变成了条件传送操作,Visual Studio 并没有什么做转换,因此并没有什么性能提升:
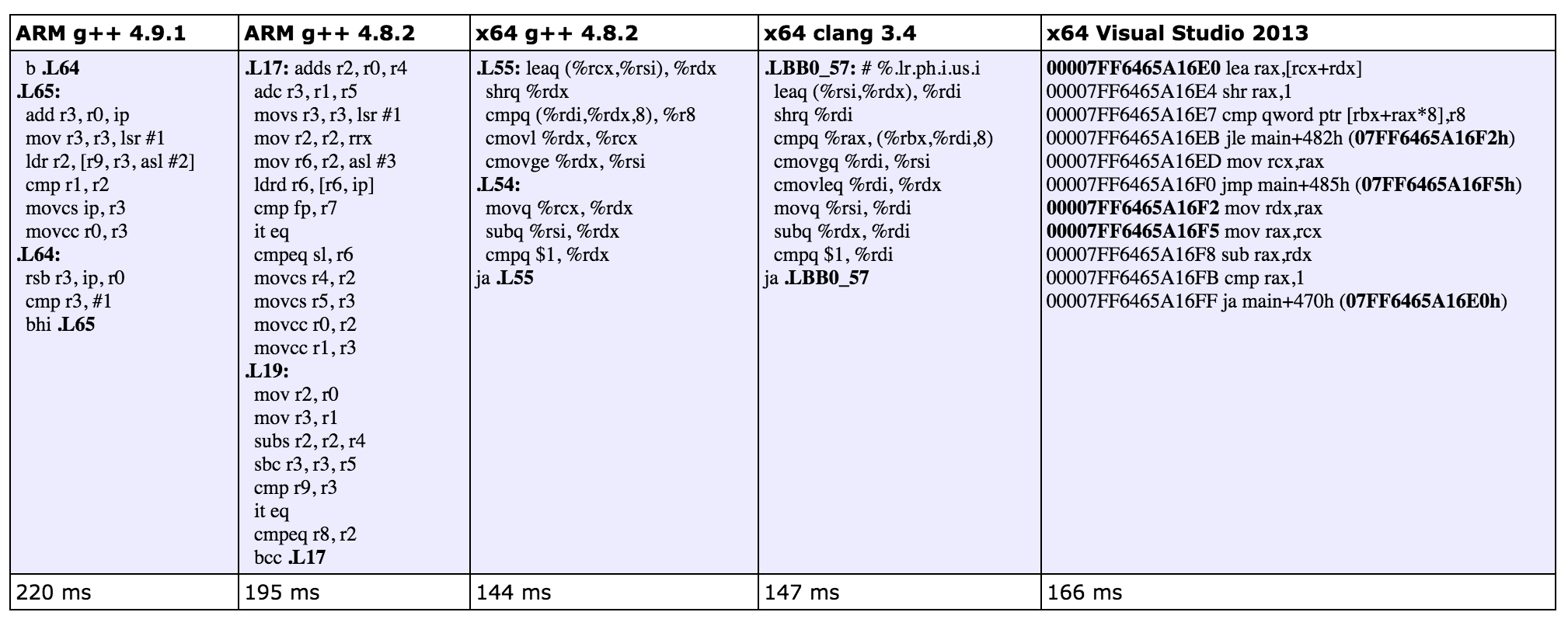
何时使用条件分支,何时使用条件传送,取决于条件是否可以被 CPU 在每次循环的时候准确的预测。
如果条件总是 true 或者 false,抑或是有一个类似下面的可预测的模式:
[true, false, true, false, true, false]
那么 CPU 的分支预测器多数时候将会正确预测。在这个例子中,条件分支耗时很少,堪比条件转移的速度。
哪种方法更快取决于微架构以及上下文。CPU 无法预测逻辑上的条件传送操作,一些微架构可以选择从昂贵的内存里提前读取一个操作数,尽管有可能这个操作数可能根本用不到。总而言之,这些测试都要根据自己的案例来定制。
如果条件语句无法被预测,那么一个条件分支就会很耗时,因为 CPU 对执行流程所做的预测都失败了,这些预测都消耗了时间却没有什么用。我们的二叉树搜索在决策要用左边分支还是右边分支的时候也是类似的情况。因此,其实条件传送是比条件分支更好的选择。
Version 3
在这个版本里,我们来完全消除 if 语句,付出的代价就是增加了一些新的非条件语句。
template <class T> INLINE size_t fast_upper_bound3(const vector<T>& vec, T value)
{
size_t size = vec.size();
size_t low = 0;
while (size > 0) {
size_t half = size / 2;
size_t other_half = size - half;
size_t probe = low + half;
size_t other_low = low + other_half;
T v = vec[probe];
size = half;
low = v >= value ? other_low : low;
}
return low;
}
我们从汇编代码里还发现 clang 编译器并不会吧三目运算符 low = v >= value ? low : other_low 转化成为条件传送操作。

我们注释掉了这个三目操作,通过调用 cmovaeq 操作,写了一个叫 choose() 内联汇���函数来替换掉这个三目运算。
template <class T> INLINE size_t choose(T a, T b, size_t src1, size_t src2)
{
#if defined(__clang__) && defined(__x86_64)
size_t res = src1;
asm("cmpq %1, %2; cmovaeq %4, %0"
:
"=q" (res)
:
"q" (a),
"q" (b),
"q" (src1),
"q" (src2),
"0" (res)
:
"cc");
return res;
#else
return b >= a ? src2 : src1;
#endif
}
我们第三次的尝试结果如下:
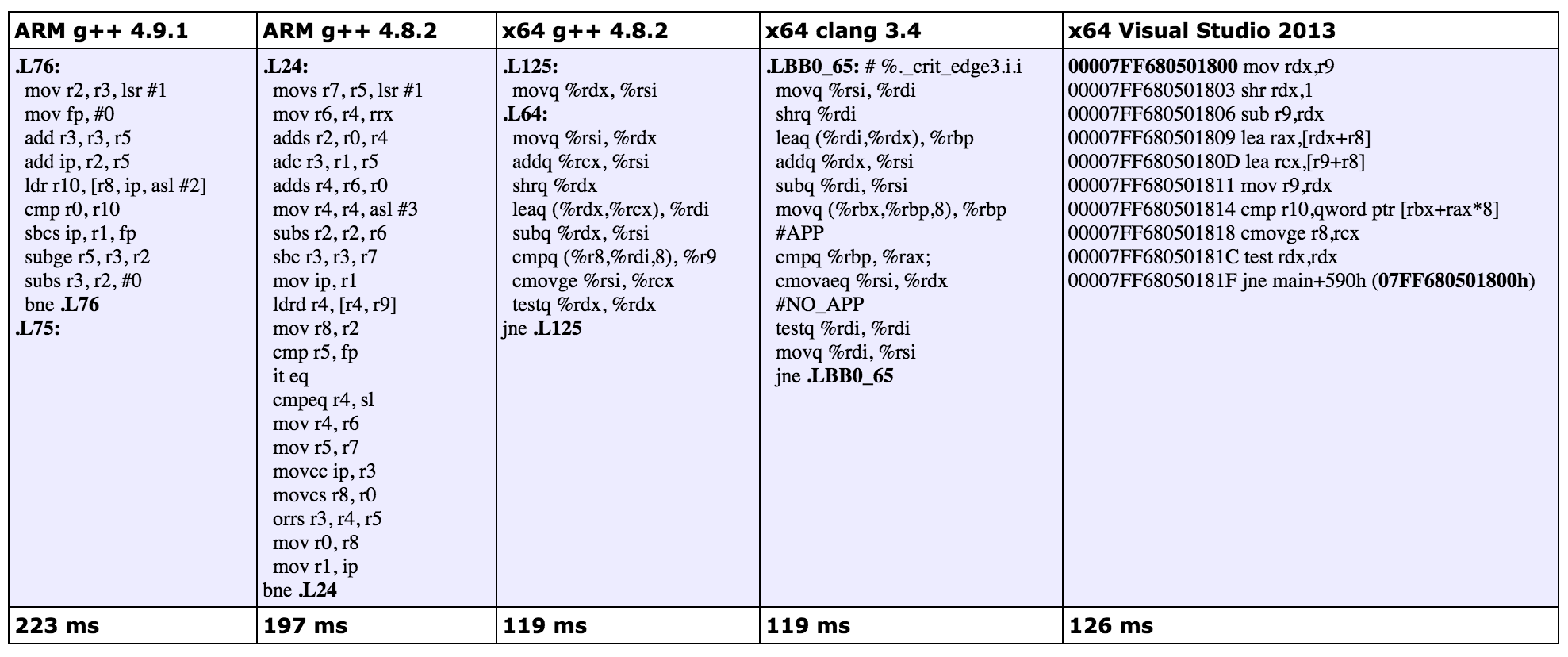
在 x64 g++ 4.8.2 和 x64 clang 3.4 的编译器上,和第二次尝试的两条指令相比,这次只生成了一句条件传送指令。这正是我们所期望的,因为我们现在在 c++ 只用一个条件赋值语句就给 low 变量赋值了。
在 ARM 上,速度并没有提升,因为一些条件传送指令被替换成了另外一些条件指令。
Version 3 的循环展开
因为我们的列表总是很长,我们用尝试循环展开技术将 while 循环拆分成 3 个重复序列:
template <class T> INLINE size_t fast_upper_bound4(const vector<T>& vec, T value)
{
size_t size = vec.size();
size_t low = 0;
while (size >= 8) {
size_t half = size / 2;
size_t other_half = size - half;
size_t probe = low + half;
size_t other_low = low + other_half;
T v = vec[probe];
size = half;
low = choose(v, value, low, other_low);
half = size / 2;
other_half = size - half;
probe = low + half;
other_low = low + other_half;
v = vec[probe];
size = half;
low = choose(v, value, low, other_low);
half = size / 2;
other_half = size - half;
probe = low + half;
other_low = low + other_half;
v = vec[probe];
size = half;
low = choose(v, value, low, other_low);
}
while (size > 0) {
size_t half = size / 2;
size_t other_half = size - half;
size_t probe = low + half;
size_t other_low = low + other_half;
T v = vec[probe];
size = half;
low = choose(v, value, low, other_low);
};
return low;
}
除了 64 位 g++ 编译器,这个优化在其他编译器上速度有微小的提升。
我们同样测试了添加 -0s 标记位(优化大小)和 -03 (优化速度) 标记位,做了 ARM 和 x64 的测试结果:

我们没有展示循环展开方案的汇编代码。
总结
以下是我们各种尝试优化的性能测试图表:

不同架构的测试
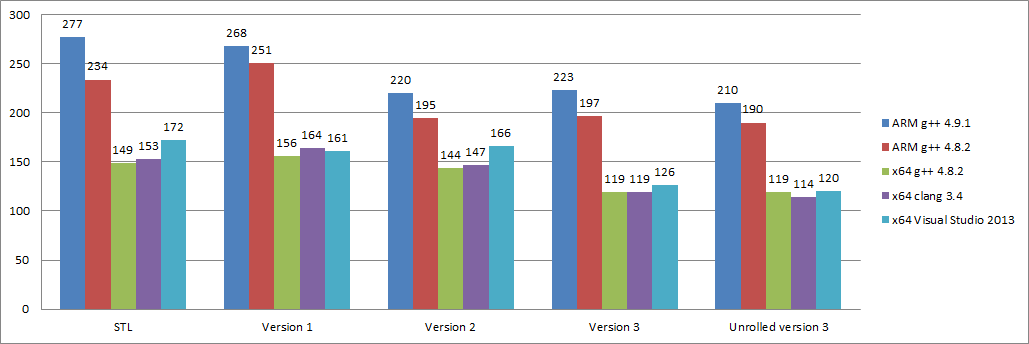
不同版本的测试
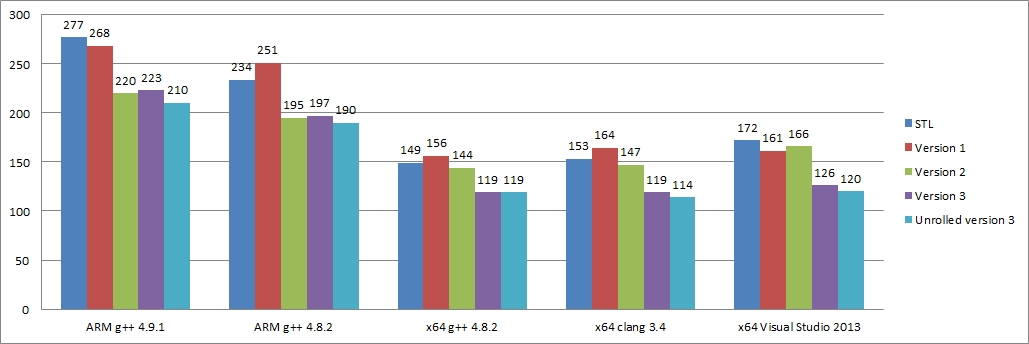
想法总结
我们开发了一种执行速度平均快于 STL 24% 的二叉树搜索算法:
(76% + 81% + 80% + 75% + 70%) / 5 = 76%
我们理解到了预测分支失败所带来的性能损耗,以及如何让编译器用条件传送替代分支预测。这种替换很麻烦,因为需要你通过生成的汇编代码才能分析的到。
一些二叉树搜索算法会以线性搜索结束查找。在循环展开的方案里,我们将无法展开的部分用了线性搜索。结果表明,平均速度提升了 1% 左右,不过很多特殊的测试用例速度慢了一些。我们期望找到一种优化方案在任何输入下都能更快!
我们还尝试了内插搜索法(interpolated binary search)。这种方法是通过列表最左和最右的数值来决定分割位置的。这种方法会用到除法操作,除法是很耗费时间的指令。只有在数据分布很均匀的时候内插搜索法法才会很有效果。
下一步
在寻找更有效率的移动数据库引擎?赶紧试试 Realm。下载 Android 和 iOS 上最新的 Realm:
和我们一起来优化这个吧!Realm 正在招贤纳士,非常期待和你一起聊聊,随时发邮件给我们:jobs@realm.io
源代码
下载完整的代码。
About the content
This content has been published here with the express permission of the author.


